The Polynomial Remainder Theorem

This section talks about the remainder theorem and how to use it to solve mathematical problems.

 

The Basics
But before we dive into the remainder theorem, lets first consider a few basic concepts regarding polynomial operations:

In the equation:

f(x) is the divided

d(x) is the divisor

q(x) is the quotient

r(x) is the remainder

 

let’s now take an example:

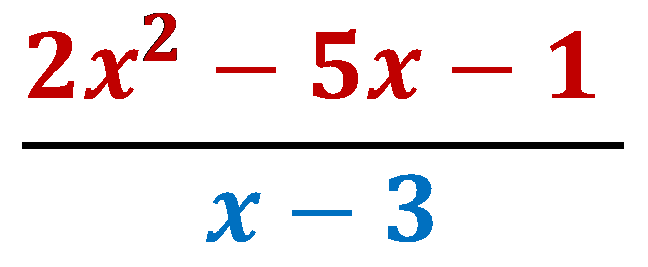
The f(x) in this example is 2x²- 5x- 1

The d(x) in this example is x- 3

 

After solving the equation:

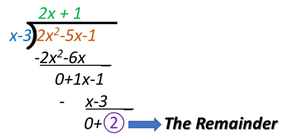
q(x) equals 2x+ 1 and r(x) equals 2

 

Let’s try another example:

Can you Identify f(x),d(x), q(x) and r(x) in this equation?

 

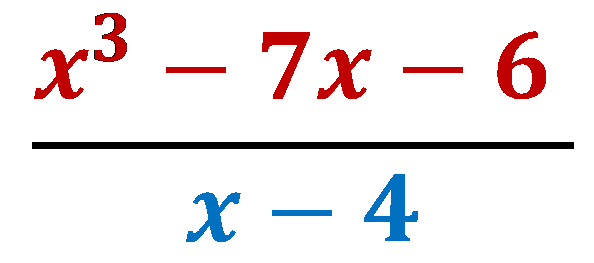
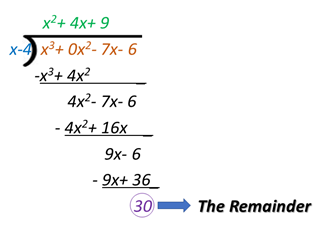
Putting It All Together

Going back to our initial formula of f(x)= d(x).q(x)+ r(x)

We can write:

2x²- 5x- 1 = (x-3)(2x+1)+ 2

X³-7x-6= (x-4)(x²+ 4x+ 9)+ 30

 

The Remainder Theorem

If a polynomial f(x) is divided by another polynomial (x- c) the remainder is always equal to f(c)

 

What this means is that (x-c) is now the divisor d(x)while f(x) remains to be the divided

I.e. f(x)= (x-c).q(x)+ r(x)

 

For this to be true (x-c) must be of degree 1, while r(x) is of degree 0. In simpler term r(x) is just a constant R

 

Now let’s assume that the value of x is the same as that of c.

If x= c then

f(c) = (c−c)·q(c) + R

f(c) = (0)·q(c) + R

f(c) = 0 + R

Therefore:

f(c) = R Where R is the remainder and this is the Reminder Theorem.

 

Using the Remainder Theorem to Work Out Remainders in Polynomial Operations

Now let’s use the remainder theorem to work out the following problems

 

Question 1: What is the remainder of:

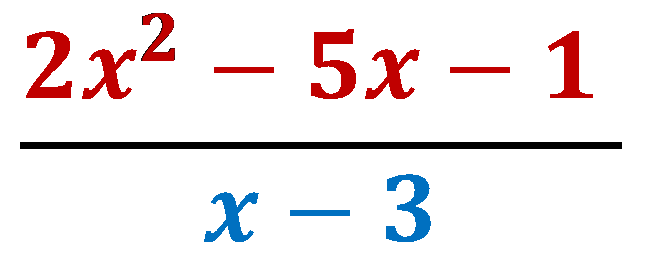
Note that c in this equation is 3

Therefore, to calculate the remainder [R or f(c)]

we simply calculate f(3) as follows. (Putting x=3 in the equation)

2(3)²− 5(3) −1

(2x9) – (5x3) −1

18−15−1

=2.

The remainder is 2

 

Question 2: What is the remainder in the equation:

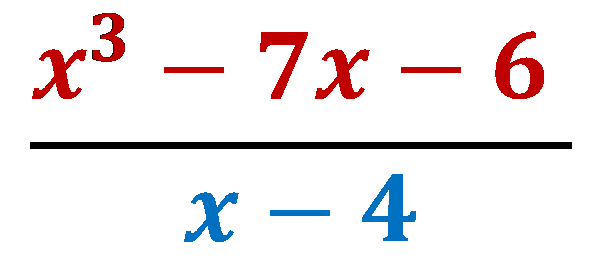
4³− 7(4)− 6

64− (7x4)− 6

64−24−6

= 30

The remainder is 30

 

Example 2

The remainder theorem shows that the value of f(x) at x=c is the same as the remainder R and we’ve already established that R= f(c)

Therefore, you might find a question asking you to find the value of f(x) as shown below:

 

Question 3: Using the Remainder Theorem work out f(x) = 2x²- 5x- 1 at x = 3.

The solution to this problem can be found by working out f(c) as described earlier

2(3)²− 5(3)− 1

(2x9) − (5x3) − 1

18−15−1

= 2

The answer can be given as f(3) = 2