From an aeroplane just over a straight road, the angles of depression of two consecutive kilometer stones situated at opposite sides of the aeroplane were found to be 60° and 30° respectively. The height (in km) of the aeroplane from the road at that instant, is
Solution:
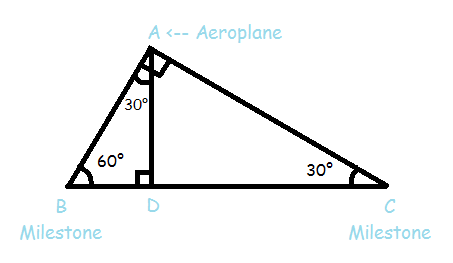
As shown in image A is the aeroplane. B and C are two consecutive milestones. So distance between them is 1km
So BC = 1
It is given that the aeroplane creates 60° and 30° angle of depression with two milestones. So we can say that angle A = 90°. (A + B + C = 180°)
So for right angle triangle ABC we can say that

Now, we want to find height of the aeroplane from the ground, so we have to find the length of AD.
Triangle ABD is right angle triangle.
So for triangle ABD, we can say that

So we can say that height of aeroplane from the ground is √3/4 km.
A tower standing on a horizontal plane subtends a certain angle at a point 160m apart from the foot of the tower. On advancing 100m towards it, the tower is found to subtend an angle twice as before. The height of the tower is
Solution:
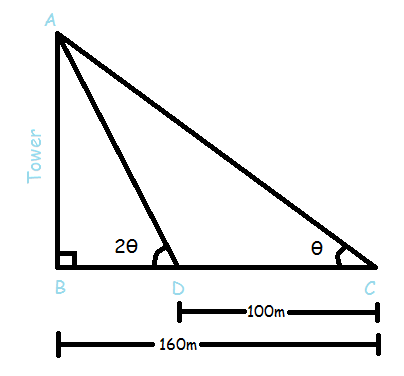
As shown in figure, AB is tower. C is the point 160m apart from the tower. Θ is the angle at point C.
Now, advancing 100m towards tower we get to the point D. 2θ is the angle at point D.
We need to find length of AB which is height of tower.
For right angle triangle ABC we can say that

And for right angle triangle ABD we can say that

But we know that
![]()
So we can write

So we can say that height of tower is 80 meters.
The length of a shadow of a vertical tower is 1/√3 times its height. The angle of elevation of the Sun is
Solution:
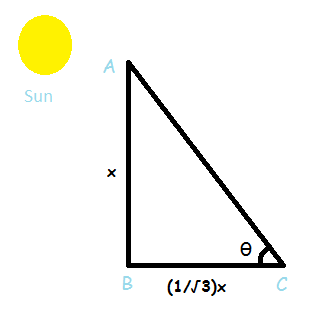
As shown in the figure, AB is the tower and let’s assume that its length is x.
BC is its shadow and its length is (1/√3)x.
We want to find angle θ.
So for right angle triangle ABC we can say that

Thus, angle of elevation of the Sun is 60°.
